데이터 분석 기록용
A/B Test와 P-value, 그리고 가설검정 본문
가설검정과 P-value
가설검정?
우리가 A/B 테스트를 진행할 때는 버전 A와 버전 B 사이 전환율($ p_a, p_b $)이 통계적으로 유의한지 확인하는 것을 목표로 진행한다.
이 경우 귀무가설($H_0$)과 대립가설($H_1$)은 아래와 같다.
$$ \begin{align*}
H_0 &: d = p_a-p_b = 0\\
H_1 &: d > 0
\end{align*} $$
가설검정을 진행할 때는 우선은 귀무가설이 기본적으로 맞다고 보고 진행한다.
실험하기 전, $ p_a, p_b $ 사이에 강한 차이가 있을 것이라고 직감적으로 알고 있어도 우리는 귀무가설을 맞다고 기본전제를 깔고 가는 것이다.
가설검정의 프로세스는 무죄 추정의 원칙을 데이터 분석에 적용하는 것과 비슷하다고 보면 된다.
결론적으로 가설검정은 무죄 추정의 원칙을 깰 수 있는 증거가 역할을 제대로 하는지 숫자로 보는 행위로 이해할 수 있다.
그리고 위에서 말한 증거로 가장 보편적으로 사용하는 것이 P-value이다.
P-value?
귀무 가설(null hypothesis)이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 '같거나 더 극단적인' 통계치가 관측될 확률
출처 - 위키피디아
P-value를 이해하기 위해서는 우선 제1종 오류($ \alpha $), 제2종 오류($ \beta $) 에 대해서 알아야 한다.
자세히 설명하기에는 글이 상당히 길어질 것 같아 자세한 내용은 다음에 이야기하고 아래 한줄로 요약해봤다.
제1종 오류($ \alpha $)는 귀무가설을 잘못 기각하는 것이고(귀무가설 True, 하지만 기각),
제2종 오류($ \beta $)는 귀무가설을 잘못 받아들이는 것(귀무가설 False, 하지만 기각X)
P-value는 제1종 오류($ \alpha $)가 일어날 수 있는 확률이라고 볼 수 있으며 귀무가설을 잘못 기각할 수 있는 확률(P-value)이 우리가 허용할 수 있는 한계치(유의수준으로 표현 ex. 5%=0.05, 1%=0.01)보다 낮다면 귀무가설을 기각할 수 있는 강한 증거로 채택할 수 있다.
여기서 나올 수 있는 생각이 하나가 있을 수 있다.
그러면 제2종 오류는 그냥 냅둬도 되나요?
답변: 당연히 아니지
$H_0$ 분포 내 $ \alpha $가 결정되는 임계값$c$보다 작은 $H_1$ 분포의 비율 $ \beta $로 표현 할 수 있다.
그리고 $ 1-\beta $는 우리는 검정력(power)로 부르고 있으며 통상적으로 0.8을 기준으로 잡고 분석을 진행한다.

그러면 또 다른 질문이 나올 수 있다.
$ \alpha $와 $\beta $가 모두 낮은게 좋은거라면 $1-\beta$를 0.8보다 높게 잡으면 좋은거 아닌가요?
답변: 위의 그림을 보면 두 가지 오류 모두 임계값$c$의 위치에 따라 Trade-off 되는 관계라 불가능함
$ 1-\beta $를 효과적으로 줄일 수 있는 방법 중 가장 잘 알려진 방법은 Sample size를 늘리는 것이다.
아래는 표본 사이즈의 변화에 따른 T분포의 변화를 그린 그래프이다.
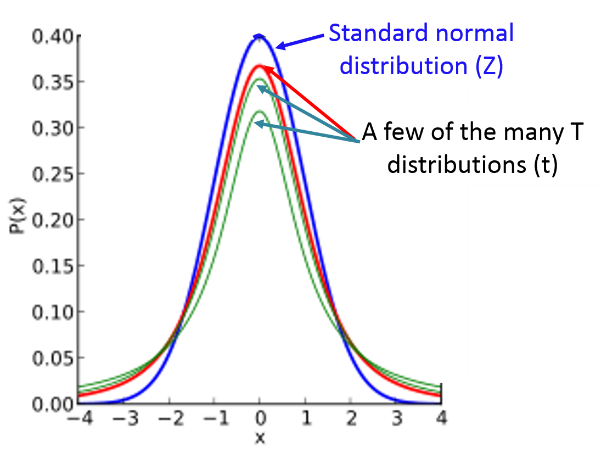
위 그림에서 볼 수 있듯이 표본 사이즈가 증가 할 수록 T분포는 Z분포에 수렴하게 변화하며 분포의 첨도가 높아져 평균 근처에 데이터가 모이기 때문에 $\beta$에 영향을 미치는 양 끝의 데이터 수가 줄어드는 것을 볼 수 있다.
적절한 표본 사이즈는 어떻게 결정 할 수 있을까?
위에서 우리는 $ \alpha $와 $\beta $가 임계값$c$를 기준으로 Trade-off되는 밀접한 관계임을 알 수 있었다.
해당 특징을 이용하여 수식을 정리하면 우리가 설정한 $ \alpha $와 $\beta $를 이용하여 표본 사이즈 $n$을 정할 수 있다.
$$ \begin{align*}
\mu_0 &: 귀무가설\ 분포\ 내 \ 평균값\\
\mu_a &: 대립가설\ 분포\ 내 \ 평균값
\end{align*} $$
$c$: $H_0$ 분포 내 $\alpha$가 결정되는 임계값
그리고 $c$를 표준정규화시켜 $ \alpha $와 $\beta $가 시작되는 지점을 정리하면 아래와 같다.
$$z_\alpha=\frac{c-\mu_0}{\sigma / \sqrt{n}}$$
$$-z_\beta=\frac{c-\mu_a}{\sigma / \sqrt{n}}$$
위의 수식을 $c$에 대해 정리하면 다음과 같다.
$$c=\mu_0+z_\alpha(\frac{\sigma}{\sqrt{n}})
=\mu_a-z_\beta(\frac{\sigma}{\sqrt{n}})$$
위의 식에서 $c$를 제외하고 $n$에 대해 다시 정리하면 $ \alpha $와 $\beta $를 이용한 표본 사이즈를 구할 수 있다.
$$n=\frac{(z_\alpha+z_\beta)^2\sigma^2}{(\mu_a-\mu_0)^2}$$
여기서 분모에서 제곱항 안에 있는 값을 효과 크기(Effect Size)라고 표현하며 A/B 테스트를 통해 확인하고 싶은 유의미한 차이를 의미한다.
그리고 A/B 테스트에서는 전환율은 비율로 표현되는데, 이항분포에서의 분산식은 아래와 같이 구할 수 있다.
$$\sigma^2=p(1-p)$$
그리고 전환율 기준으로 변환된 식은 아래와 같이 표현될 것이다.
$$n=\frac{(z_\alpha+z_\beta)^2(p_a(1-p_a)+p_b(1-p_b))^2}{(p_b-p_a)^2}$$
장황하게 설명했지만 간편하게 표본 사이즈를 계산할 수 있는 사이트들은 도처에 널려있다.
예시
무엇보다 이렇게 표본 사이즈를 계산하는 이유는 실험이 유의미 할때까지 얼마나 기다려야 되는지를 정량적으로 알 수 있다는 것이다.
필요한 표본만큼 인원이 모이지 않은 상태에서 실험을 마무리하는 경우는 대부분 분석가의 확증편향에 따라 조기에 마감하는 경우가 많을 것이다. 하지만 실험 초기 단계에서는 P-value가 낮지만 실험이 진행될수록 결과가 바뀌는 경우는 상당히 빈번하기 때문에 인내심을 가지고 실험이 끝날때까지 기다리는 것이 중요하다.
Reference
AB TEST Sample Size 구하기
A/B 테스트에서 p-value에 휘둘리지 않기
'데이터 분석' 카테고리의 다른 글
| ChatGPT assistant API + Streamlit 사용후기 (0) | 2024.03.24 |
|---|---|
| 첫 데이터 로그 설계 실무와 그에 대한 퇴고 (1) | 2024.03.23 |
| 연애 시뮬레이션 코딩하고 결과 확인하기 (0) | 2023.07.23 |
| 모바일 앱 제품 내 지표분석 예시 (0) | 2023.05.04 |
| A/B Test 기초 (0) | 2023.04.28 |


